- Kapalı devre için
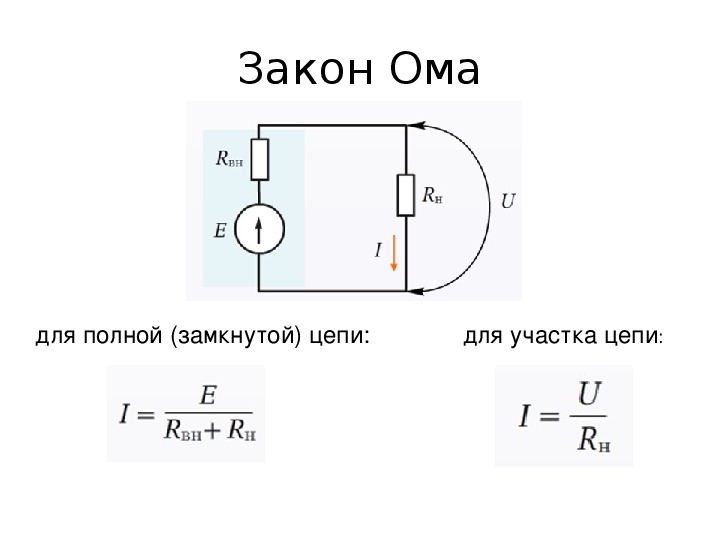
- Ayrı bölüm ve komple elektrik devresi
- Elektrik devresinin akım bölümünün hesaplanması
- Tam bir zincir için hesaplama seçeneği
- Yasanın bir değişken üzerindeki etkisi
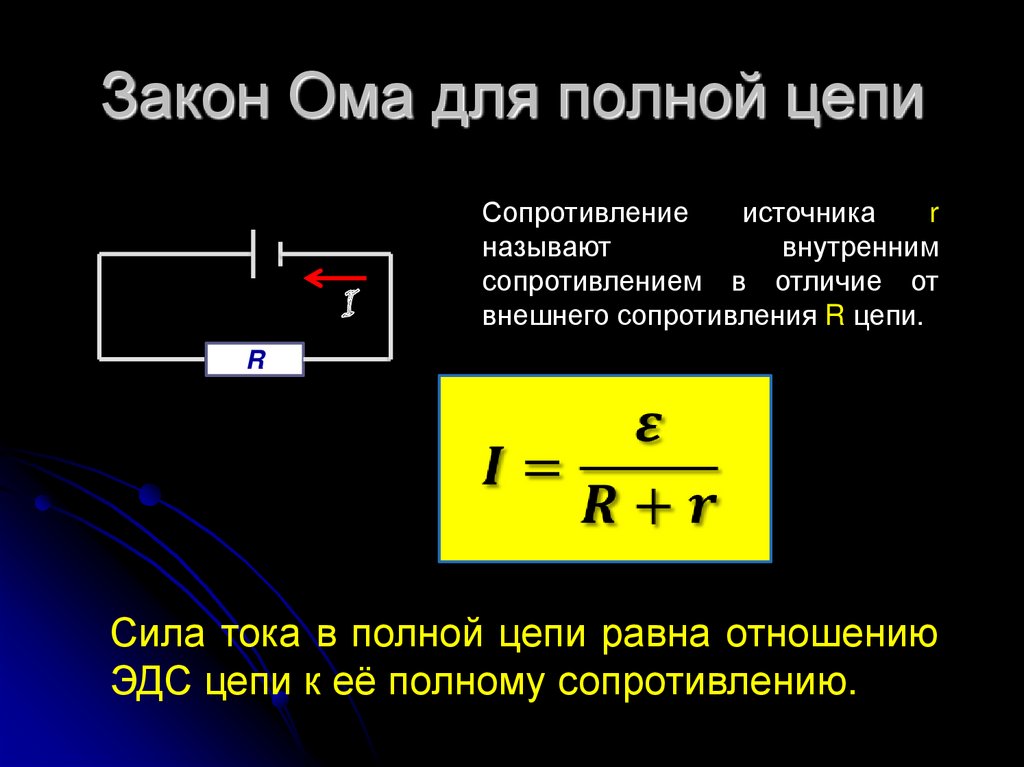
- Tam bir devrede EMF kaynağı
- R - elektrik direnci
- DC devresinin düzgün olmayan bölümü
- Elemanların seri ve paralel bağlantısı
- Seri bağlı dirençli elemanlar zinciri
- Paralel bağlı dirençli elemanlar zinciri
- Hukukun integral ve diferansiyel biçimleri
- Akım ve direnci anlama
- Alternatif akım için Ohm yasası
- Ohm kanunu oluştuğunda
- Kirchhoff yasaları.
- Temel konseptler
- Güç ve gerginlik
- İletken direnci
- Ohm kanunu yorumu
- Paralel ve seri bağlantı
- seri bağlantı
- Paralel bağlantı
- Bize paralel ve seri bağlantı sağlayan nedir?
- İdeal EMF kaynağı
- diferansiyel formda
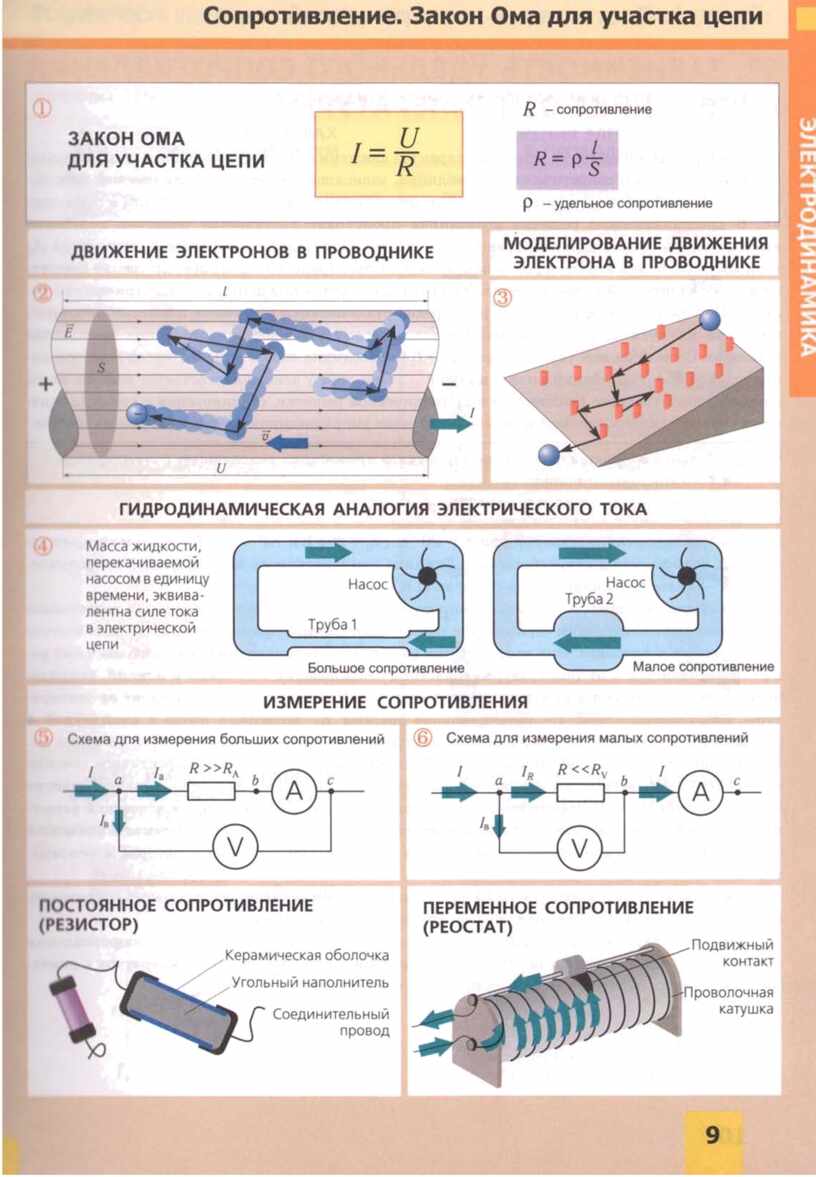
Kapalı devre için
Kapalı devre, içinden akımın dolaştığı kapalı bir elektrik bağlantısı anlamına gelir. Çemberin bir ucundan diğer ucuna geçecek şekilde birbirine bağlanan ve devreyi tamamlayan bir dizi tel olduğunda, bu kapalı bir devre olacaktır.
EMF (E) - volt olarak gösterilir ve ölçülür ve zamanla değişen bir manyetik alanın bir elektrik akımı oluşturacağını belirten Faraday yasasına göre bir pil veya manyetik kuvvet tarafından üretilen voltajı ifade eder.
Sonra: E = IR + Ir
E \u003d I (R + r)
ben \u003d E / (R + r)
Nerede: r, akım kaynağının direncidir.
Bu ifade, Ohm'un kapalı döngü devreleri yasası olarak bilinir.
heterojen zincir
Ayrı bölüm ve komple elektrik devresi
Bir bölüme veya tüm devreye uygulanan Ohm yasası, iki hesaplama seçeneğinde düşünülebilir:
- Ayrı kısa bölüm. EMF kaynağı olmayan bir devrenin parçasıdır.
- Bir veya daha fazla bölümden oluşan eksiksiz bir zincir. Bu aynı zamanda kendi iç direncine sahip bir EMF kaynağını da içerir.
Elektrik devresinin akım bölümünün hesaplanması
Bu durumda, I \u003d U / R temel formülü uygulanır, burada I akım gücü, U voltaj, R dirençtir. Buna göre, Ohm yasasının genel kabul görmüş yorumu formüle edilebilir:
Bu formülasyon, grafik tasarımda sözde "papatya" üzerinde sunulan diğer birçok formülün temelidir. P sektöründe - güç belirlenir, I, U ve R sektörlerinde - akım gücü, voltaj ve direnç ile ilgili eylemler gerçekleştirilir.
Her ifade - hem temel hem de ek, devrede kullanılması amaçlanan elemanların kesin parametrelerini hesaplamanıza izin verir.
Elektrik devreleriyle çalışan uzmanlar, şekilde gösterilen üçgen yöntemini kullanarak herhangi bir parametrenin hızlı bir şekilde belirlenmesini gerçekleştirir.
Hesaplamalar, bölümün elemanlarını bağlayan iletkenlerin direncini dikkate almalıdır. Farklı malzemelerden yapıldıkları için bu parametre her durumda farklı olacaktır.Tam bir devre oluşturmak gerekirse, ana formül, örneğin bir pil gibi bir voltaj kaynağının parametreleriyle desteklenir.
Tam bir zincir için hesaplama seçeneği
Tam bir devre, bir voltaj kaynağı (EMF) ile birlikte tek bir bütün halinde birleştirilen ayrı bölümlerden oluşur. Böylece, bölümlerin mevcut direnci, bağlı kaynağın iç direnci ile tamamlanır. Bu nedenle, daha önce tartışılan ana yorum aşağıdaki gibi olacaktır: I = U / (R + r). Burada, EMF kaynağının dirençli göstergesi (r) zaten eklenmiştir.
Saf fizik açısından, bu gösterge çok küçük bir değer olarak kabul edilir. Bununla birlikte, pratikte, karmaşık devreleri ve devreleri hesaplarken, ek direnç işin doğruluğunu etkilediği için uzmanlar bunu dikkate almak zorunda kalırlar. Ayrıca her kaynağın yapısı oldukça heterojendir, sonuç olarak bazı durumlarda direnç oldukça yüksek oranlarla ifade edilebilir.
Yukarıdaki hesaplamalar DC devrelerle ilgili olarak yapılır. Alternatif akım ile işlemler ve hesaplamalar farklı bir şemaya göre yapılır.
Yasanın bir değişken üzerindeki etkisi
Alternatif akım ile devrenin direnci, aktif direnç ve reaktif dirençli yükten oluşan sözde empedans olacaktır. Bu, endüktif özelliklere ve sinüzoidal bir akım değerine sahip elemanların varlığından kaynaklanmaktadır. Voltaj da kendi anahtarlama yasalarına göre hareket eden bir değişkendir.
Bu nedenle, Ohm yasası AC devre tasarımı, belirli etkiler dikkate alınarak hesaplanır: akımın büyüklüğünü voltajdan yönlendirmek veya geciktirmek, ayrıca aktif ve reaktif gücün varlığı.Buna karşılık, reaktans, endüktif veya kapasitif bileşenleri içerir.
Tüm bu fenomenler, Z'nin empedans olduğu Z \u003d U / I veya Z \u003d R + J * (XL - XC) formülüne karşılık gelecektir; R - aktif yük; XL, XC - endüktif ve kapasitif yükler; J düzeltme faktörüdür.
Tam bir devrede EMF kaynağı
Kapalı bir devrede elektrik akımının oluşması için, bu devre, kutupları arasında yük aktarma işinin gerçekleşeceği en az bir özel eleman içermelidir. Bu elemanın içinde yük taşıyan kuvvetler bunu elektrik alanına karşı yapar, bu da doğalarının elektrikten farklı olması gerektiği anlamına gelir. Bu nedenle, bu tür güçlere üçüncü taraf denir.
Pirinç. 1. Fizikte dış kuvvetler.
Bir elektrik alanının hareketine karşı yükleri aktarmak için dış kuvvetlerin çalıştığı bir elektrik devresinin elemanına akım kaynağı denir. Ana özelliği, dış kuvvetlerin büyüklüğüdür. Bunu karakterize etmek için özel bir ölçü getirildi - Elektromotor Kuvvet (EMF), $\mathscr{E}$ harfi ile gösterilir.
Akım kaynağının EMF'sinin değeri, yükün aktarılması için dış kuvvetlerin bu yükün değerine oranına eşittir:
$$\mathscr{E}={A_{st}\overq}$$
EMF'nin anlamı, elektrik voltajının anlamına çok yakın olduğu için (hatırlayın, voltaj, yükü taşıyan elektrik alanı tarafından yapılan işin bu yükün değerine oranıdır), o zaman EMF, voltaj gibi ölçülür. Volt:
$$1B={J\overCl}$$
Gerçek bir akım kaynağının ikinci en önemli elektriksel özelliği, iç direncidir.Yükler terminaller arasında aktarıldığında, EMF kaynağının maddesi ile etkileşime girerler ve bu nedenle elektrik akımı kaynağı da bir miktar direnç gösterir. İç direnç, sıradan direnç gibi, ohm cinsinden ölçülür, ancak küçük Latin harfi $r$ ile gösterilir.

Pirinç. 2. Akım kaynaklarına örnekler.
R - elektrik direnci
Direnç, voltajın tersidir ve bir cismi akan sudaki harekete karşı hareket ettirmenin etkisiyle karşılaştırılabilir. R'nin birimi Om'dur ve Yunanca büyük harf Omega ile gösterilir.
Direncin tersi (1/R), bir nesnenin Siemens birimlerinde ifade edilen bir yükü iletme yeteneğini ölçen iletkenlik olarak bilinir.
Kullanılan geometrik olarak bağımsız niceliğe özdirenç denir ve genellikle Yunan sembolü r ile gösterilir.
Ek Bilgiler. Ohm yasası, elektrik şebekesinin çalışmasının, güç hesaplamasını basitleştiren üç önemli göstergesinin oluşturulmasına yardımcı olur. Diyot, transistör ve benzeri elemanlara sahip tek taraflı ağlar için geçerli değildir. Ayrıca tristörlerin örnek olduğu lineer olmayan elemanlara da bu elemanların direnç değeri verilen farklı voltaj ve akımla değiştiği için uygulanamaz.
Daha yüksek frekanslarda, dağıtılmış davranış baskın hale gelir. Aynı şey çok uzun elektrik hatlarında da olur. 60 Hz gibi düşük bir frekansta bile 30 km gibi çok uzun bir iletim hattı dağıtık bir yapıya sahiptir.Bunun ana nedeni, devrelerde yayılan etkin elektrik sinyallerinin bir elektromanyetik dalganın bulaştırdığı volt ve amper değil, elektromanyetik dalgalar olmasıdır. İletkenler sadece dalgalar için kılavuz görevi görür. Bu nedenle, örneğin, bir koaksiyel kablo, DC direnci ihmal edilebilir olsa bile Z = 75 ohm gösterecektir.
Ohm yasası, elektrik mühendisliğinin temel yasasıdır. Tüm elektrik devrelerinde ve elektronik bileşenlerde çok sayıda pratik uygulamaya sahiptir.
Ohm yasasının uygulanmasının en yaygın örnekleri:
- Elektrikli ısıtıcıya sağlanan güç. Isıtıcı bobinin direnci ve uygulanan voltaj göz önüne alındığında, o ısıtıcıya verilen güç hesaplanabilir.
- Sigorta seçimi. Elektronik cihazlarla seri olarak bağlanan koruma bileşenleridir. Sigortalar/CB'ler amper cinsinden derecelendirilir. Geçerli sigorta değeri, Ohm yasası kullanılarak hesaplanır.
- Elektronik cihazların tasarımı. Dizüstü bilgisayarlar ve cep telefonları gibi elektronik cihazlar, belirli bir akım derecesine sahip bir DC güç kaynağı gerektirir. Tipik cep telefonu pilleri 0.7-1A gerektirir.Bu bileşenlerden geçen akımın hızını kontrol etmek için bir direnç kullanılır. Ohm kanunu, tipik bir devrede anma akımını hesaplamak için kullanılır.
Bir zamanlar, Ohm'un sonuçları elektrik alanındaki yeni araştırmalar için bir katalizör oldu ve bugün modern elektrik mühendisliği onlara dayandığından önemlerini kaybetmedi. 1841'de Om, Kraliyet Cemiyeti'nin en yüksek onuru olan Copley Madalyası ile ödüllendirildi ve "Om" terimi 1872 gibi erken bir tarihte bir direniş birimi olarak kabul edildi.
DC devresinin düzgün olmayan bölümü
Heterojen bir yapı, iletkenlere ve elemanlara ek olarak bir akım kaynağının bulunduğu devrenin böyle bir bölümüne sahiptir. Bu alandaki toplam akım gücünü hesaplarken EMF'si dikkate alınmalıdır.
Heterojen bir sitenin ana parametrelerini ve süreçlerini tanımlayan bir formül vardır: q = q0 x n x V. Göstergeleri aşağıdaki gibi karakterize edilir:
- Hareketli yükler (q) sürecinde belirli bir yoğunluk kazanırlar. Performansı, iletkenin (S) akım gücüne ve kesit alanına bağlıdır.
- Belirli bir konsantrasyon (n) koşulları altında, tek bir zaman diliminde hareket ettirilen birim yüklerin (q0) sayısını doğru bir şekilde belirtmek mümkündür.
- Hesaplamalar için, iletken şartlı olarak bir miktar hacme (V) sahip silindirik bir bölüm olarak kabul edilir.
İletkeni aküye bağlarken, ikincisi bir süre sonra boşalacaktır. Yani elektronların hareketi yavaş yavaş yavaşlar ve sonunda tamamen durur. Bu, elektronların birbirleriyle ve diğer faktörlerle çarpışmasını önleyen iletkenin moleküler kafesi ile kolaylaştırılır. Bu tür bir direnişin üstesinden gelmek için ek olarak belirli üçüncü taraf kuvvetlerinin uygulanması gerekir.
Hesaplamalar sırasında bu kuvvetler Coulomb kuvvetlerine eklenir. Ek olarak, bir birim yükü q 1. noktadan 2. noktaya aktarmak için, A1-2 veya sadece A12 işini yapmak gerekli olacaktır. Bu amaçla bir potansiyel farkı (ϕ1 - ϕ2) oluşturulur. Bir doğru akım kaynağının etkisi altında, devre boyunca yükleri hareket ettiren bir EMF ortaya çıkar. Toplam stresin büyüklüğü, yukarıda belirtilen tüm kuvvetlerden oluşacaktır.
Hesaplamalarda DC kaynağına yapılan bağlantının polaritesi dikkate alınmalıdır. Terminaller değiştirildiğinde, EMF de değişecek, yüklerin hareketini hızlandıracak veya yavaşlatacaktır.
Elemanların seri ve paralel bağlantısı
Bir elektrik devresinin (bir devrenin bölümü) elemanları için, karakteristik bir moment bir seri veya paralel bağlantıdır.
Buna göre, her bağlantı tipine, akım akışının ve gerilim beslemesinin farklı bir doğası eşlik eder. Bu hesapta, Ohm kanunu, elementleri dahil etme seçeneğine bağlı olarak farklı şekillerde de uygulanır.
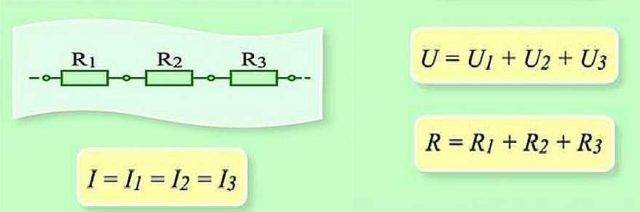
Seri bağlı dirençli elemanlar zinciri
Seri bağlantı (iki bileşenli bir devrenin bölümü) ile ilgili olarak şu ifade kullanılır:
- ben = ben1 = ben2 ;
- U = U1 + U2 ;
- R=R1 + R2
Bu formülasyon, seri bağlı dirençli bileşenlerin sayısından bağımsız olarak, devrenin bir bölümünde akan akımın değerini değiştirmediğini açıkça göstermektedir.
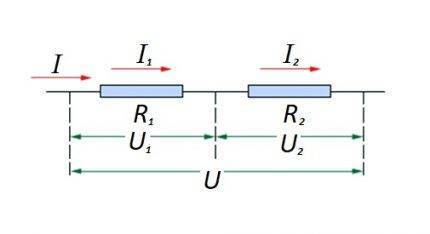 Direnç elemanlarının bir devre bölümünde birbirine seri bağlanması. Bu seçeneğin kendi hesaplama yasası vardır. Şemada: I, I1, I2 - akım akışı; R1, R2 - dirençli elemanlar; U, U1, U2 - uygulanan voltaj
Direnç elemanlarının bir devre bölümünde birbirine seri bağlanması. Bu seçeneğin kendi hesaplama yasası vardır. Şemada: I, I1, I2 - akım akışı; R1, R2 - dirençli elemanlar; U, U1, U2 - uygulanan voltaj
Devrenin aktif dirençli bileşenlerine uygulanan voltaj miktarı toplamıdır ve EMF kaynağının değerine eklenir.
Bu durumda, her bir bileşen üzerindeki voltaj: Ux = I * Rx.
Toplam direnç, devrenin tüm dirençli bileşenlerinin değerlerinin toplamı olarak düşünülmelidir.
Paralel bağlı dirençli elemanlar zinciri
Dirençli bileşenlerin paralel bir bağlantısı olması durumunda, Alman fizikçi Ohm yasasına göre formülasyon adil kabul edilir:
- ben = ben1 + ben2 … ;
- U = U1 = U2 … ;
- 1/R = 1/R1 + 1 / Sağ2 + …
Paralel ve seri bağlantılar kullanıldığında, "karma" tipteki devre bölümlerini derleme seçenekleri hariç tutulmaz.
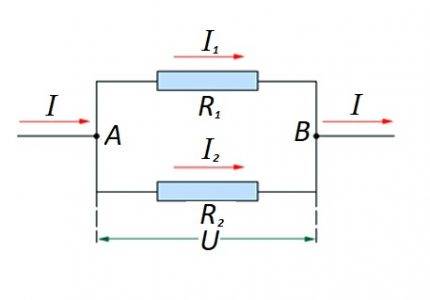 Direnç elemanlarının bir devre bölümünde birbirine paralel bağlanması. Bu seçenek için kendi hesaplama kanunu uygulanır. Şemada: I, I1, I2 - akım akışı; R1, R2 - dirençli elemanlar; U - uygulanan voltaj; A, B - giriş / çıkış noktaları
Direnç elemanlarının bir devre bölümünde birbirine paralel bağlanması. Bu seçenek için kendi hesaplama kanunu uygulanır. Şemada: I, I1, I2 - akım akışı; R1, R2 - dirençli elemanlar; U - uygulanan voltaj; A, B - giriş / çıkış noktaları
Bu tür seçenekler için hesaplama genellikle paralel bağlantının direnç derecesinin ilk hesaplanmasıyla gerçekleştirilir. Daha sonra seri bağlı direncin değeri sonuca eklenir.
Hukukun integral ve diferansiyel biçimleri
Hesaplamalı yukarıdaki noktaların tümü, tabiri caizse “homojen” bir yapıya sahip iletkenlerin elektrik devrelerinin bir parçası olarak kullanıldığı koşullara uygulanabilir.
Bu arada, pratikte, genellikle, iletkenlerin yapısının farklı alanlarda değiştiği bir şematik yapı ile uğraşmak zorundadır. Örneğin, daha büyük bir kesite sahip teller kullanılır veya tam tersine, farklı malzemeler temelinde yapılan daha küçük teller kullanılır.
Bu tür farklılıkları hesaba katmak için, sözde "diferansiyel-integral Ohm yasası"nın bir varyasyonu vardır. Sonsuz küçük bir iletken için akım yoğunluğu seviyesi, yoğunluk ve iletkenlik değerine bağlı olarak hesaplanır.
Diferansiyel hesaplamada şu formül alınır: J = ό * E
İntegral hesaplaması için sırasıyla formül: I * R = φ1 - φ2 + έ
Bununla birlikte, bu örnekler yüksek matematik okuluna oldukça yakındır ve aslında basit bir elektrikçinin gerçek uygulamasında kullanılmazlar.
Akım ve direnci anlama
Elektrik akımı kavramıyla başlayalım.Kısacası, metallerle ilgili olarak elektrik akımı, elektronların - negatif yüklü parçacıkların yönlendirilmiş hareketidir. Genellikle küçük daireler olarak temsil edilirler. Sakin bir durumda, sürekli yön değiştirerek kaotik bir şekilde hareket ederler. Belirli koşullar altında - potansiyel bir farkın ortaya çıkması - bu parçacıklar belirli bir yönde belirli bir harekete başlar. Bu hareket elektrik akımıdır.
Daha açık hale getirmek için, elektronları bir düzleme dökülen su ile karşılaştırabiliriz. Uçak sabit olduğu sürece su hareket etmez. Ancak, bir eğim ortaya çıkar çıkmaz (potansiyel bir fark ortaya çıktı), su hareket etmeye başladı. Elektronlarda da durum aynıdır.
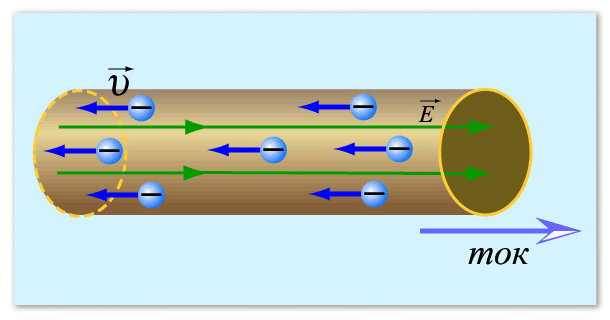
Bir elektrik akımı bu şekilde hayal edilebilir.
Şimdi direncin ne olduğunu ve neden mevcut güçle geri bildirim aldıklarını anlamamız gerekiyor: direnç ne kadar yüksekse, akım o kadar düşük olur. Bildiğiniz gibi, elektronlar bir iletken boyunca hareket eder. Genellikle bunlar metal tellerdir, çünkü metaller elektriği iletme konusunda iyi bir yeteneğe sahiptir. Metalin yoğun bir kristal kafese sahip olduğunu biliyoruz: yakın ve birbirine bağlı birçok parçacık. Metal atomları arasında yol alan elektronlar, onlarla çarpışır ve bu da hareket etmelerini zorlaştırır. Bu, bir iletkenin uyguladığı direnci göstermeye yardımcı olur. Şimdi, direnç ne kadar yüksek olursa, akım gücü o kadar düşük olur - daha fazla parçacık, elektronların yolu aşması daha zor, daha yavaş yapıyorlar. Bu halledilmiş gibi görünüyor.
Bu bağımlılığı ampirik olarak test etme arzunuz varsa, değişken bir direnç bulun, seri olarak bir direnç - bir ampermetre - bir akım kaynağı (pil) bağlayın.Devreye bir anahtar eklemek de istenir - sıradan bir geçiş anahtarı.
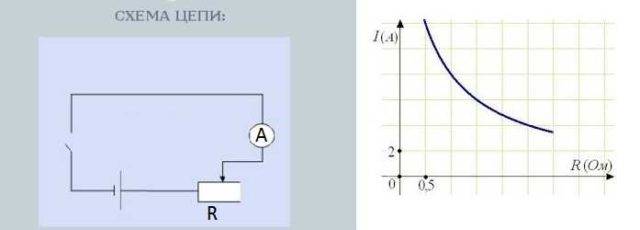
Akımın dirence bağımlılığını test etmek için devre
Direnç düğmesinin çevrilmesi direnci değiştirir. Aynı zamanda mevcut gücü ölçen ampermetre üzerindeki okumalar da değişir. Dahası, direnç ne kadar büyük olursa, ok o kadar az sapar - o kadar az akım. Direnç ne kadar düşük olursa, ok o kadar fazla sapar - akım daha büyüktür.
Akımın dirence bağımlılığı neredeyse doğrusaldır, yani grafiğe neredeyse düz bir çizgi olarak yansıtılır. Neden neredeyse - bu ayrıca tartışılmalıdır, ama bu başka bir hikaye.
Alternatif akım için Ohm yasası
AC devreleri hesaplanırken direnç kavramı yerine "empedans" kavramı getirilir. Empedans Z harfi ile gösterilir, R yükünün aktif direncini içerir.a ve reaktans X (veya Rr). Bu, sinüzoidal akımın (ve diğer formların akımlarının) şeklinden ve endüktif elemanların parametrelerinden ve ayrıca anahtarlama yasalarından kaynaklanmaktadır:
- Bir endüktif devredeki akım anında değişemez.
- Kapasitanslı bir devredeki voltaj anında değişemez.
Böylece akım, gerilimi geciktirmeye veya yönlendirmeye başlar ve görünen güç, aktif ve reaktif olarak ikiye ayrılır.
U=I/Z
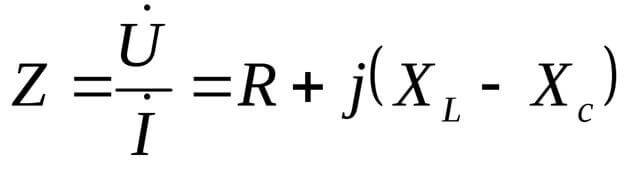
XL ve XC yükün reaktif bileşenleridir.
Bu bağlamda, cosФ değeri tanıtılır:
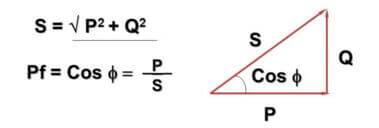
Burada - Q - alternatif akım ve endüktif kapasitif bileşenlerden kaynaklanan reaktif güç, P - aktif güç (aktif bileşenlerde dağıtılır), S - görünen güç, cosФ - güç faktörü.
Formülün ve temsilinin Pisagor teoremi ile kesiştiğini fark etmiş olabilirsiniz. Bu doğrudur ve Ф açısı, yükün reaktif bileşeninin ne kadar büyük olduğuna bağlıdır - ne kadar büyükse, o kadar büyüktür.Pratikte bu, şebekede gerçekten akan akımın bir ev sayacı tarafından dikkate alınandan daha büyük olmasına ve işletmeler tam güç için ödeme yapmasına neden olur.
Bu durumda, direnç karmaşık biçimde sunulur:
Burada j, karmaşık denklem biçimleri için tipik olan hayali bir birimdir. Daha az yaygın olarak i olarak adlandırılır, ancak elektrik mühendisliğinde alternatif akımın etkin değeri de belirtilir, bu nedenle karıştırılmaması için j kullanmak daha iyidir.
Sanal birim √-1'dir. Kare alırken böyle bir sayının olmaması mantıklıdır, bu da olumsuz bir "-1" sonucuna neden olabilir.
Ohm kanunu oluştuğunda
İdeal koşulları yaratmak kolay değildir. Saf iletkenlerde bile elektrik direnci sıcaklığa göre değişir. Azalması, serbest yüklerin hareketini basitleştiren kristal kafes moleküllerinin aktivitesini en aza indirir. Belirli bir "donma" seviyesinde süperiletkenliğin etkisi meydana gelir. Isıtıldığında ters etki (iletkenliğin bozulması) gözlenir.
Aynı zamanda elektrolitler, metaller ve belirli seramik türleri, akım yoğunluğundan bağımsız olarak elektrik direncini korur. Belirli bir sıcaklık rejimini korurken parametrelerin kararlılığı, Ohm yasasının formüllerini ek düzeltmeler olmadan uygulamayı mümkün kılar.
Yarı iletken malzemeler ve gazlar, değişen elektrik direnci ile karakterize edilir. Bu parametre, kontrol hacmindeki akım yoğunluğundan önemli ölçüde etkilenir. Performans özelliklerini hesaplamak için özel hesaplama yöntemleri uygulanmalıdır.
Alternatif akım düşünülürse hesaplama yöntemi düzeltilir.Bu durumda, reaktif bileşenlerin varlığı dikkate alınmalıdır. Direncin dirençli doğası ile, Ohm yasasının formüllerine dayalı olarak kabul edilen hesaplama teknolojilerini uygulamak mümkündür.
Kirchhoff yasaları.
Dağıtım
elektrik devresinin dallarındaki akımlar
Kirchhoff'un birinci yasasına uyar,
ve gerilimlerin bölümler üzerindeki dağılımı
zincir Kirchhoff'un ikinci yasasına uyar.
Kirchhoff yasaları
Ohm yasası ile birlikte ana
elektrik devreleri teorisinde.
İlk
Kirchhoff yasası:
Cebirsel
düğümdeki akımların toplamı sıfırdır:
i
= 0 (19)
Neresi
i
belirli bir düğümde birleşen dalların sayısıdır.
yani toplama
dallardaki akımlara kadar uzanır,
düşünüldüğünde birleşen
düğüm.
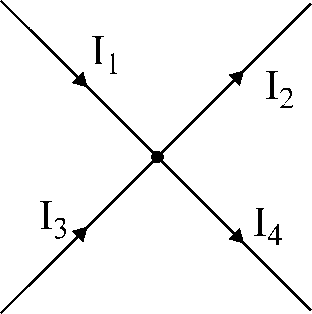
Şekil 17. illüstrasyon
Kirchhoff'un birinci yasasına göre.
Sayı
birinciye göre derlenen denklemler
Kirchhoff yasası şu formülle belirlenir:
nup
= Yok
– 1,
Neresi
hayır
dikkate alınan zincirdeki düğüm sayısıdır.
Akım belirtileri
denklemler seçilen dikkate alınarak alınır
pozitif yön. İşaretler
Akımlar aynıysa akımlar aynıdır
buna göre yönlendirilmiş
düğüm.
Örneğin,
Şekil 17'de gösterilen düğüm için:
düğüme akan akımlara işaretler atarız
"+" ve düğümden akan akımlara - işaretler
«-».
sonra denklem
Kirchhoff'un birinci yasasına göre yazılacak
Yani:
ben1
- BEN2
+ ben3
- BEN4
= 0.
denklemler,
Kirchhoff'un birinci yasasına göre derlenir,
düğümler denir.
Bu
yasa, düğümde olduğu gerçeğini ifade eder
elektrik yükü birikmez
ve tüketilmez. elektrik miktarı
siteye gelen ücretler toplamına eşittir
düğümü bir ve aynı şekilde terk eden ücretler
aynı zaman aralığı.
İkinci
Kirchhoff yasası:
Cebirsel
emf toplamı herhangi bir kapalı devrede
zincir düşmelerin cebirsel toplamına eşittir
bu devrenin elemanlarındaki voltaj:
Ui
=
Ei
IiRi=Ei(20)
Neresi
i
- eleman numarası (direnç veya
gerilim kaynağı) dikkate alındığında
kontur.
**Sayı
ikinciye göre derlenen denklemler
Kirchhoff yasası şu formülle belirlenir:
nup
= Nb
- Hayır
+ 1 – Ned.s.
Neresi
not
- elektrik devresinin dallarının sayısı;
hayır
- düğüm sayısı;
Ned.s.
ideal emf kaynaklarının sayısıdır.
Şekil 18. illüstrasyon
Kirchhoff'un ikinci yasasına göre.
İçin,
ikinci yasayı doğru yazmak
Belirli bir kontur için Kirchhoff, aşağıdaki
aşağıdaki kurallara uyun:
-
keyfi olarak
kontur baypas yönünü seçin,
örneğin, saat yönünde (Şek. 18). -
emf
ve eşleşen voltaj düşüşleri
seçilen yön ile yönde
baypas ile bir ifadede yazılır
"+" işareti; eğer e.f.s. ve voltaj düşüşü
yön uyuşmaz
kontur, sonra bir işaretten önce gelirler.
«-».
Örneğin,
Şekil 18'in konturu için Kirchhoff'un ikinci yasası
aşağıdaki gibi yazılacaktır:
sen1
– U2
+ U3
= E1
– E3
– E4
(21)
Denklem (20) olabilir
olarak yeniden yazın:
(Ui
– Ei)
= 0 (22)
Neresi
(Ü
-E)
- daldaki gerginlik.
Sonuç olarak,
Kirchhoff'un ikinci yasası formüle edilebilir
Aşağıdaki şekilde:
Cebirsel
herhangi bir daldaki gerilimlerin toplamı
kapalı döngü sıfırdır.
Potansiyel
daha önce tartışılan diyagram hizmet eder
ikincisinin grafiksel yorumu
Kirchhoff yasası.
Görev numarası 1.
AT
Şekil 1'deki devreye I akımları verilmiştir.1
ve ben3,
direnç ve emf akımları belirle
ben4,
ben5,
ben6
; a noktaları arasındaki voltaj
ve B
Eğer ben1
= 10mA,
ben3
= -20 mA,
R4
= 5kOhm,
E5
= 20B,
R5
= 3kOhm,
E6
= 40B,
R6
= 2kOhm.
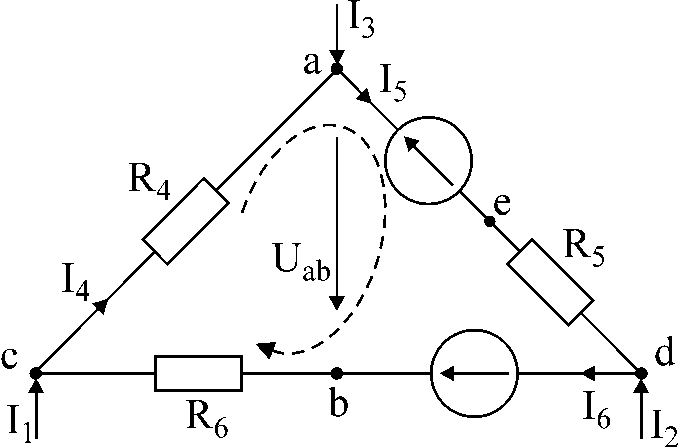
Şekil 1
Çözüm:
-
verilen için
kontur, göre iki denklem oluştururuz
Kirchhoff'un birinci yasası ve bir - göre
ikinci. kontur yönü
okla gösterilir.

AT
elde ettiğimiz çözüm sonucunda: I6
= 0; ben4
= 10mA;
ben5
= -10mA
-
sormak
noktalar arasındaki voltaj yönü
a
ve B
"a" noktasından
"b"yi işaret etmek
-Uab.
Bu voltaj denklemden bulunabilir.
Kirchhoff'un ikinci yasası:
ben4R4
+ Uab
+ ben6R6
= 0
senab
= - 50V.
Görev numarası 2.
İçin
Şekil 2'deki diyagramlar, aşağıdakilere göre denklemler çizer.
Kirchhoff yasaları ve bilinmeyenleri belirleme
puan.
Verilen:
ben1
= 20mA;
ben2
= 10mA
R1
= 5kOhm,
R3
= 4kOhm,
R4
= 6kOhm,
R5
= 2kOhm,
R6
= 4kΩ.
İncir. 2
Çözüm:
Düğüm sayısı
denklemler - 3, kontur denklemlerinin sayısı
– 1.
Unutma!
Denklemi ikinciye göre derlerken
Kirchhoff yasası, konturu seçiyoruz,
hangi mevcut kaynakları içermez.
Konturun yönü şekilde gösterilmiştir.
AT
bu devrenin, I dallarının akımları1
ve ben2.
Bilinmeyen
akımlar
ben3,
ben4,
ben5,
ben6.

karar vermek
sistem, şunu elde ederiz: I3
= 13,75 mA;
ben4
= -3.75mA;
ben5
= 6.25mA;
ben6
= 16.25mA.
Temel konseptler
Kapalı bir devre elektronların devredeki yüksek potansiyelden daha düşük potansiyele hareket etmesine izin verdiğinde elektrik akımı akar. Başka bir deyişle, akım, onları harekete geçirecek enerjiye sahip bir elektron kaynağının yanı sıra, eksiklikleri ile karakterize edilen negatif yüklerin geri dönüş noktası gerektirir. Fiziksel bir fenomen olarak, bir devredeki akım üç temel nicelik ile karakterize edilir:
- Gerilim;
- mevcut güç;
- elektronların hareket ettiği bir iletkenin direnci.
Güç ve gerginlik
Akım gücü (I, Amper cinsinden ölçülür), birim zaman başına devredeki bir yer boyunca hareket eden elektronların (yük) hacmidir.Başka bir deyişle, ölçüm I, hareket halindeki elektronların sayısının belirlenmesidir.
Terimin yalnızca harekete atıfta bulunduğunu anlamak önemlidir: örneğin, bağlı olmayan bir pilin terminallerindeki statik yükler, ölçülebilir bir I değerine sahip değildir. Bir yönde akan akıma doğrudan (DC) denir ve Periyodik olarak değişen yön, alternatif (AC) olarak adlandırılır. Voltaj, basınç gibi bir fenomen veya yerçekimi etkisi altındaki nesnelerin potansiyel enerjisindeki fark olarak gösterilebilir.
Bu dengesizliği yaratmak için öncelikle uygun koşullarda hareket halinde gerçekleşecek olan enerjiyi harcamanız gerekir. Örneğin, bir yükün bir yükseklikten düşmesi durumunda, onu kaldırmak için çalışma yapılır, galvanik pillerde, jeneratörlerde kimyasal enerjinin dönüştürülmesi nedeniyle terminallerdeki potansiyel fark oluşur - maruz kalmanın bir sonucu olarak bir elektromanyetik alan
Stres, basınç gibi bir fenomen veya yerçekimi etkisi altındaki nesnelerin potansiyel enerjisindeki fark olarak gösterilebilir. Bu dengesizliği yaratmak için öncelikle uygun koşullarda hareket halinde gerçekleşecek olan enerjiyi harcamanız gerekir. Örneğin, bir yükün bir yükseklikten düşmesinde, kaldırma işi gerçekleştirilir, galvanik pillerde, jeneratörlerde kimyasal enerjinin dönüştürülmesi nedeniyle terminallerdeki potansiyel fark oluşur - bir maruz kalma sonucu elektromanyetik alan.
İletken direnci
Sıradan bir iletken ne kadar iyi olursa olsun, hareketlerine bir miktar direnç göstermeden elektronların geçmesine asla izin vermez.Bu karşılaştırma mükemmel olmayacak olsa da, direnci mekanik sürtünmenin bir analoğu olarak düşünmek mümkündür. Akım bir iletkenden geçtiğinde, bir miktar potansiyel fark ısıya dönüşür, bu nedenle direnç boyunca her zaman bir voltaj düşüşü olacaktır. Elektrikli ısıtıcılar, saç kurutma makineleri ve diğer benzer cihazlar, yalnızca elektrik enerjisini ısı şeklinde dağıtmak için tasarlanmıştır.
Basitleştirilmiş direnç (R olarak gösterilir), bir devrede elektron akışının ne kadar geciktirildiğinin bir ölçüsüdür. Ohm cinsinden ölçülür. Bir direncin veya başka bir elemanın iletkenliği iki özellikle belirlenir:
- geometri;
- malzeme.
Hidrolik benzetmenin açıkça gösterdiği gibi şekil son derece önemlidir: suyu uzun, dar bir borudan itmek, suyu kısa, geniş bir borudan itmekten çok daha zordur. Malzemeler belirleyici bir rol oynamaktadır. Örneğin, elektronlar bir bakır telde serbestçe hareket edebilir, ancak şekilleri ne olursa olsun kauçuk gibi yalıtkanlardan hiç akamazlar. Geometri ve malzemeye ek olarak iletkenliği etkileyen başka faktörler de vardır.
Ohm kanunu yorumu
Yüklerin hareketini sağlamak için devreyi kapatmanız gerekir. Ek gücün yokluğunda, akım uzun süre var olamaz. Potansiyeller hızla eşitlenecek. Devrenin çalışma modunu korumak için ek bir kaynağa (jeneratör, pil) ihtiyaç vardır.
Tam devre, tüm bileşenlerin toplam elektrik direncini içerecektir. Doğru hesaplamalar için iletkenlerdeki, dirençli elemanlardaki ve bir güç kaynağındaki kayıplar dikkate alınır.
Belirli bir akım gücü için ne kadar voltaj uygulanması gerektiği aşağıdaki formülle hesaplanır:
U=I*R.
Benzer şekilde, ele alınan ilişkiler yardımıyla devrenin diğer parametreleri belirlenir.
Paralel ve seri bağlantı
Elektrikte, elemanlar seri olarak - birbiri ardına veya paralel olarak - bu, birkaç girişin bir noktaya bağlandığı ve aynı elemanlardan gelen çıkışların diğerine bağlandığı zamandır.
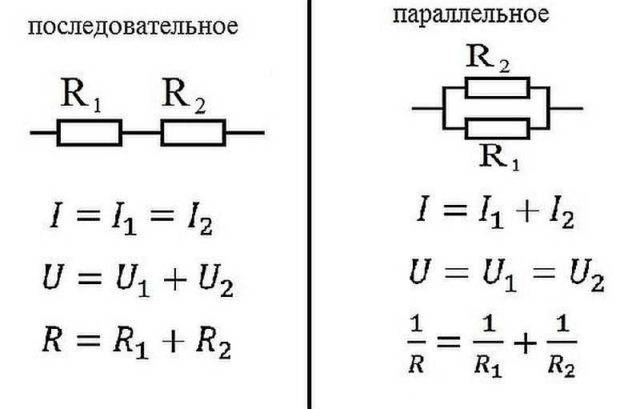
Paralel ve seri bağlantı için Ohm yasası
seri bağlantı
Ohm yasası bu durumlar için nasıl çalışır? Seri bağlandığında, eleman zincirinden geçen akım aynı olacaktır. Elemanları seri bağlanmış bir devrenin bir bölümünün gerilimi, her bölümdeki gerilimlerin toplamı olarak hesaplanır. Bu nasıl açıklanabilir? Bir elemanın içinden akımın akışı, yükün bir kısmının bir kısmından diğerine aktarılmasıdır. Demek istediğim, bu biraz iş. Bu işin boyutu gerilimdir. Bu, stresin fiziksel anlamıdır. Bu açıksa, devam ederiz.
Devrenin bu bölümünün seri bağlantısı ve parametreleri
Seri bağlandığında, yükü her bir eleman üzerinden sırayla aktarmak gerekir. Ve her öğede, bu belirli bir iş hacmidir. Ve zincirin tüm bölümündeki iş miktarını bulmak için, işi her bir öğeye eklemeniz gerekir. Böylece, toplam voltajın, elemanların her birindeki voltajların toplamı olduğu ortaya çıktı.
Aynı şekilde - toplama yardımı ile - devre bölümünün toplam direnci de bulunur. Nasıl hayal edebiliyorsun? Eleman zincirinden akan akım sırayla tüm dirençlerin üstesinden gelir. Birer birer. Yani, üstesinden geldiği direnci bulmak için dirençleri toplamak gerekir. Aşağı yukarı böyle.Matematiksel türetme daha karmaşıktır ve bu yasanın mekanizmasını anlamak daha kolaydır.
Paralel bağlantı
Paralel bağlantı, iletkenlerin / elemanların başlangıçlarının bir noktada birleştiği ve diğerinde uçlarının bağlandığı zamandır. Bu tür bileşikler için geçerli olan yasaları açıklamaya çalışacağız. Akım ile başlayalım. Elemanların bağlantı noktasına belirli bir büyüklükte bir akım verilir. Ayrılır, tüm iletkenlerden akar. Bundan, bölümdeki toplam akımın, her bir elemandaki akımın toplamına eşit olduğu sonucuna varıyoruz: I = I1 + I2 + I3.
Şimdi voltaj için. Voltaj bir yükü hareket ettirmek için iş ise, bir yükü hareket ettirmek için gereken iş herhangi bir eleman üzerinde aynı olacaktır. Yani paralel bağlı her elemanın gerilimi aynı olacaktır. U=U1=U2=U3. Bir zincir bölümü için Ohm yasasının açıklanması durumundaki kadar eğlenceli ve görsel değil, ancak anlayabilirsiniz.
Paralel Bağlantı Yasaları
Direnç için işler biraz daha karmaşık. İletkenlik kavramını tanıtalım. Bu, bir yükün bu iletkenden geçmesinin ne kadar kolay veya zor olduğunu gösteren bir özelliktir. Direnç ne kadar düşük olursa, akımın geçmesi o kadar kolay olur. Bu nedenle iletkenlik - G - direncin tersi olarak hesaplanır. Formülde şöyle görünür: G = 1/R.
Neden iletkenlikten bahsediyoruz? Çünkü elemanların paralel bağlı olduğu bir bölümün toplam iletkenliği, her bir bölümün iletkenliklerinin toplamına eşittir. G = G1 + G2 + G3 - anlaşılması kolay. Akımın bu paralel elemanlar düğümünün üstesinden ne kadar kolay geleceği, her bir elemanın iletkenliğine bağlıdır. Bu yüzden katlanmaları gerektiği ortaya çıktı.
Artık direnişe geçebiliriz.İletkenlik direncin tersi olduğu için şu formülü elde edebiliriz: 1/R = 1/R1 + 1/R2 + 1/R3.
Bize paralel ve seri bağlantı sağlayan nedir?
Teorik bilgi iyidir, ancak pratikte nasıl uygulanır? Her türden eleman paralel ve seri olarak bağlanabilir. Ancak doğrusal öğeleri tanımlayan yalnızca en basit formülleri düşündük. Doğrusal elemanlar, "dirençler" olarak da adlandırılan dirençlerdir. İşte öğrendiklerinizi nasıl kullanacağınız:
Büyük değerli direnç yoksa, ancak birkaç küçük direnç varsa, birkaç direnç seri bağlanarak istenen direnç elde edilebilir. Gördüğünüz gibi, bu yararlı bir tekniktir.
Pillerin ömrünü uzatmak için paralel bağlanabilirler. Bu durumda, Ohm yasasına göre voltaj aynı kalacaktır (gerilimi bir multimetre ile ölçerek emin olabilirsiniz). Ve ikili pilin "ömrü", birbirinin yerini alacak iki öğenin ömründen çok daha uzun olacaktır.
Sadece dikkat: sadece aynı potansiyele sahip güç kaynakları paralel bağlanabilir. Yani, ölü ve yeni bir pil bağlanamaz.
Yine de bağlanırsanız, daha fazla şarjı olan pil, daha az şarjlı olanı şarj etme eğiliminde olacaktır. Sonuç olarak, toplam ücretleri düşük bir değere düşecektir.
Genel olarak, bunlar bu bileşiklerin en yaygın kullanımlarıdır.
İdeal EMF kaynağı
Elektromotor kuvvet (E), kapalı bir yük taşıyıcı devresindeki hareket üzerindeki dış kuvvetlerin etkisinin derecesini belirleyen fiziksel bir niceliktir. Başka bir deyişle, akımın iletkenden ne kadar güçlü bir şekilde akma eğilimi EMF'ye bağlı olacaktır.
Bu tür anlaşılmaz olayları açıklarken, yerli okul öğretmenleri hidrolik analojiler yöntemine başvurmayı severler. İletken bir boruysa ve elektrik akımı içinden akan su miktarıysa, EMF bir pompanın sıvıyı pompalamak için geliştirdiği basınçtır.
Elektromotor kuvvet terimi, voltaj gibi bir kavramla ilgilidir. O, EMF, ayrıca volt cinsinden ölçülür (birim - "V"). Pil, jeneratör veya güneş paneli olsun, her güç kaynağının kendi elektromotor kuvveti vardır. Genellikle bu EMF, çıkış voltajına (U) yakındır, ancak her zaman bundan biraz daha azdır. Bu, voltajın kaçınılmaz olarak düştüğü kaynağın iç direncinden kaynaklanır.
Bu nedenle ideal EMF kaynağı, gerçek dünyada yeri olmayan soyut bir kavram veya fiziksel bir modeldir, çünkü Rin pilinin iç direnci çok düşük olmasına rağmen mutlak sıfırdan farklıdır.
İdeal ve gerçek emf kaynağı
diferansiyel formda
İletken genellikle homojen olmadığından ve onu mümkün olan en küçük bölümlere ayırmak gerekeceğinden, formül sıklıkla diferansiyel bir biçimde sunulur. İçinden geçen akım büyüklük ve yön ile ilişkilidir, bu nedenle skaler bir miktar olarak kabul edilir. Bir telden geçen akım bulunacağı zaman, tüm bireysel akımların cebirsel toplamı alınır. Bu kural sadece skaler büyüklükler için geçerli olduğundan, akım da skaler büyüklük olarak alınır. Akım dI = jdS'nin kesitten geçtiği bilinmektedir. Üzerindeki voltaj Edl'ye eşittir, daha sonra sabit kesitli ve eşit uzunlukta bir tel için oran doğru olacaktır:
 diferansiyel formu
diferansiyel formu
Bu nedenle, akımın vektör biçiminde ifadesi şöyle olacaktır: j = E.
Önemli! Metalik iletkenlerde sıcaklık arttıkça iletkenlik azalırken yarı iletkenlerde artar. Omov yasası katı orantılılık göstermiyor
Büyük bir metal ve alaşım grubunun direnci, mutlak sıfıra yakın bir sıcaklıkta kaybolur ve bu sürece süperiletkenlik denir.